Table Of Content
Since each treatment occurs once in each block, the number of test specimens is the number of replicates. Many times there are nuisance factors that are unknown and uncontrollable (sometimes called a “lurking” variable). We always randomize so that every experimental unit has an equal chance of being assigned to a given treatment. Randomization is our insurance against a systematic bias due to a nuisance factor.
4 Outlook: Multiple Block Factors
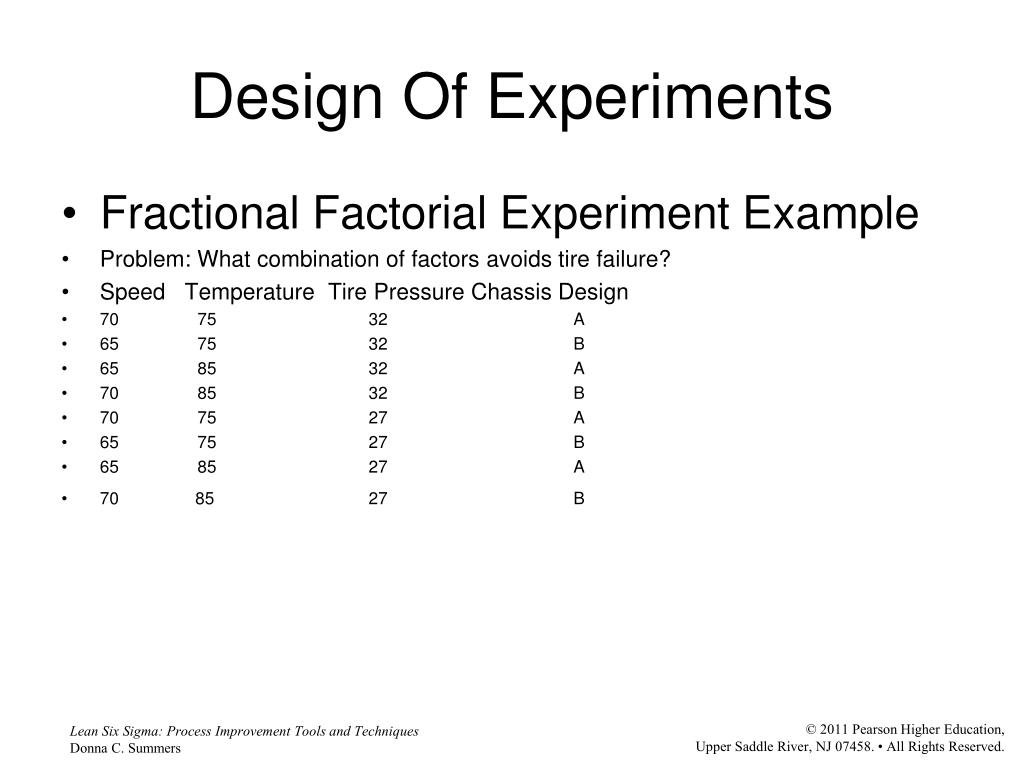
Here we have four blocks and within each of these blocks is a random assignment of the tips within each block. Back to the hardness testing example, the experimenter may very well want to test the tips across specimens of various hardness levels. To conduct this experiment as a RCBD, we assign all 4 tips to each specimen. In this example we wish to determine whether 4 different tips (the treatment factor) produce different (mean) hardness readings on a Rockwell hardness tester.
Identify nuisance variables
What we did here was use the one-way analysis of variance instead of the two-way to illustrate what might have occurred if we had not blocked, if we had ignored the variation due to the different specimens. An alternate way of summarizing the design trials would be to use a 4x3 matrix whose 4 rows are the levels of the treatment X1 and whose columns are the 3 levels of the blocking variable X2. The cells in the matrix have indices that match the X1, X2 combinations above. Implementing blocking in experimental design involves a series of steps to effectively control for extraneous variables and enhance the precision of treatment effect estimates. We illustrate the extension using our drug-diet example from Chapter 6 where three drugs were combined with two diets.

Block Randomization
If this point is missing we can substitute x, calculate the sum of squares residuals, and solve for x which minimizes the error and gives us a point based on all the other data and the two-way model. We sometimes call this an imputed point, where you use the least squares approach to estimate this missing data point. To compare the results from the RCBD, we take a look at the table below.
6.1 Construction of BIBDs
We do not have observations in all combinations of rows, columns, and treatments since the design is based on the Latin square. Together, you can see that going down the columns every pairwise sequence occurs twice, AB, BC, CA, AC, BA, CB going down the columns. The combination of these two Latin squares gives us this additional level of balance in the design, than if we had simply taken the standard Latin square and duplicated it. A Graeco-Latin square is orthogonal between rows, columns, Latin letters and Greek letters.
Want to Pass Your Six Sigma Exam the First Time through?
The Analysis of Variance table shows three degrees of freedom for Tip three for Coupon, and the error degrees of freedom is nine. The ratio of mean squares of treatment over error gives us an F ratio that is equal to 14.44 which is highly significant since it is greater than the .001 percentile of the F distribution with three and nine degrees of freedom. Variability between blocks can be large, since we will remove this source of variability, whereas variability within a block should be relatively small. In the first example provided above, the sex of the patient would be a nuisance variable. For example, consider if the drug was a diet pill and the researchers wanted to test the effect of the diet pills on weight loss. The explanatory variable is the diet pill and the response variable is the amount of weight loss.
Complete randomization can however createimbalanced designs, for example, grouping all samples of the samecondition in the same batch. Block randomization is an approach thatcan prevent severe imbalances in sample allocation with respect toboth known and unknown confounders. This feature provides the readerwith an introduction to blocking and randomization, and insights intohow to effectively organize samples during experimental design, withspecial considerations with respect to proteomics. Blocking is a useful technique to control systematic variation in experiments.
Construction of symmetric paired choice experiments: minimising runs and maximising efficiency Humanities and ... - Nature.com
Construction of symmetric paired choice experiments: minimising runs and maximising efficiency Humanities and ....
Posted: Tue, 03 Oct 2023 07:00:00 GMT [source]
The model is specified as y ~ drug + Error(cage+rep/litter) or y ~ drug + (1|cage)+(1|rep/litter). The most important example is the balanced incomplete block design (BIBD), where each pair of treatments is allocated to the same number of blocks, and so are therefore all individual treatments. This specific type of balance ensures that pair-wise contrasts are all estimated with the same precision, but precision decreases if more than two treatment groups are compared. A typical example of a non-random classification factor is the sex of an animal. The Hasse diagrams in Figure 7.6 show an experiment design to study the effects of our three drugs on both female and male mice. Each treatment group has eight mice, with half of them female, the other half male.
2.3 Contrasts
We now illustrate the GLM analysis based on the missing data situation - one observation missing (Batch 4, pressure 2 data point removed). The least squares means as you can see (below) are slightly different, for pressure 8700. What you also want to notice is the standard error of these means, i.e., the S.E., for the second treatment is slightly larger.
Most experiments have to accountfor control variables when estimating the treatment effects. Somecommon control variables are technical in nature, such as proteasebatches, freezer locations, and biobanks, but sample characteristicssuch as sex, age, and patient ancestry also commonly fall into thiscategory. As the complexity of the design increases, it is commonthat not all samples can be processed at the same time in the sameway at the same location. The sets of samples created by this processare referred to as batches, and this becomes yet another control variableto account for. Since \(\lambda\) is not an integer there does not exist a balanced incomplete block design for this experiment. Seeing as how the block size in this case is fixed, we can achieve a balanced complete block design by adding more replicates so that \(\lambda\) equals at least 1.
Design and realization of data mining simulation and methodological models - ScienceDirect.com
Design and realization of data mining simulation and methodological models.
Posted: Wed, 01 Nov 2023 15:14:45 GMT [source]
The treatment factor levels are the Latin letters in the Latin square design. The number of rows and columns has to correspond to the number of treatment levels. So, if we have four treatments then we would need to have four rows and four columns in order to create a Latin square. This gives us a design where we have each of the treatments and in each row and in each column. For example, we might be concerned about the effect of litters on our drug comparisons, but suspect that the position of the cage in the rack also affects the observations.
Many industrial and human subjects experiments involve blocking, or when they do not, probably should in order to reduce the unexplained variation. Here are the main steps you need to take in order to implement blocking in your experimental design. Blocking is one of those concepts that can be difficult to grasp even if you have already been exposed to it once or twice. Because the specific details of how blocking is implemented can vary a lot from one experiment to another.
Now let us introduce a machine drift (Figure Figure11C,G) that causesthe mass spectrometer todetect slightly less of the protein over time. For the ordered allocation,the observed protein abundances show almost no difference betweenthe two group means (Figure Figure11D). Conversely, the difference in group means for the randomizedallocation is nearly the same as the “true” difference(Figure Figure11H), and onlyhas added variance caused by the machine drift (Figure Figure22).
In a completely randomized $2\times2$ factorial layout (no blocks), you would completely randomly decide the order in which the breads are baked. For each loaf, you would preheat the oven, open a package of bread dough, and bake it. This would involve running the oven 160 times, once for each loaf of bread. Graphical exploration of the data is a little more problematic in this example. As each treatment does not occur in each block, box plots such as Figure 3.2 are not as informative. Do compounds three and four have higher average wear because they were the only compounds to both occur in blocks 3 and 4?
The common use of this design is where you have subjects (human or animal) on which you want to test a set of drugs -- this is a common situation in clinical trials for examining drugs. This is a simple extension of the basic model that we had looked at earlier. The row and column and treatment all have the same parameters, the same effects that we had in the single Latin square. In a Latin square, the error is a combination of any interactions that might exist and experimental error. Therefore, one can test the block simply to confirm that the block factor is effective and explains variation that would otherwise be part of your experimental error. However, you generally cannot make any stronger conclusions from the test on a block factor, because you may not have randomly selected the blocks from any population, nor randomly assigned the levels.
No comments:
Post a Comment